Théorie sur le calcul d'ensoleillement
Fichier Excel
Version: 1.0
Date de création: 15/04/13
Dernière modification: 31/05/13
Téléchargé 4880 fois
Introduction
Selon l’OMM, la durée de l’ensoleillement représente la période durant laquelle le rayonnement solaire direct dépasse le seuil de 120 W/m². Dans la réalité, le calcul est bien complexe. Prenez par exemple une belle matinée d'hiver, vous pouvez être sûr que le seuil du rayonnement solaire ne dépasse pas les 120 W/m² et pourtant le soleil est bien présent. A l'inverse, un 21 juin même nuageux dépassera ce seuil à midi.
La méthode décrite ici va permettre le calcul d'un seuil de radiation solaire à chaque instant, directement lié à la position du soleil.
ATTENTION: les calculs ci-dessous font références à des angles en degrés. Si ces calculs sont codés dans un language informatique, il y a de grande chance que les fonctions Sinus et Cosinus prennent en argument des angles en radians. Il faudra donc multiplier chaque angle par π/180.
Déclinaison solaire
La déclinaison solaire δ correspond à l’angle que forme la direction Terre-Soleil par rapport au plan de l’équateur terrestre.
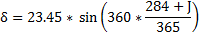
J correpond au jour de l'année (de 1 à 366).
Inclinaison solaire
L'inclinaison solaire α correspond à l'angle entre le soleil est l'horizon.
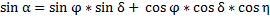
Avec φ la latitude (ex : 48.65°N pour Plévenon) et η l'angle horaire définie par:
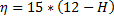
H étant le temps solaire (en heure décimale, ex: 6.12) défini par:
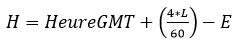
On additionne à l'heure GMT le décalage horaire induit par la longitude L (soit 4min/°).
E est le résultat de l'équation du temps. Vu la précision des calculs ici, on considère que E=0.
Flux solaire
Le flux solaire est le rayonnement solaire (en W/m²) présent à l'entrée de l'atmosphère.
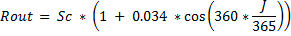
Sc est la constante solaire, définie par l'OMM, qui est égale à 1367 W/m² et J le jour de l'année.
Influence de l'atmophère et de l'altitude de la mesure
L'atmosphère terrestre, de part sa composition, attenue fortement la puissance du rayonnement solaire. C'est pourquoi il est nécessaire de calculer un coefficient d'attenuation qui sera lui aussi dépendant de la position du soleil, du jour de l'année...etc. De même que la hauteur de la mesure influe aussi étant donné que plus haut on se situe, plus la couche de l'atmophère à traversé est moins épaisse.
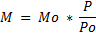
P est la pression relative, Po la pression absolue.
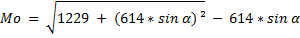
Pour ma part je considère que le facteur de correction de l'altitude est négligeable. On a donc M = Mo.
Rayonnement solaire global
Le rayonnement solaire global est le résultat de l'addition du rayonnement directe, du rayonnement solaire réfléchi et du rayonnement solaire diffus. Ici la mesure est effectué à l'horizontal, le rayonnement réfléchi est donc nul.
Rayonnement directe
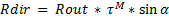
Avec τ = 0.6
Rayonnement diffus
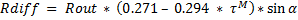
On en déduit ainsi le rayonnement solaire global:
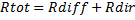
Calcul de la durée d'ensoleillement
A chaque réception d'une donnée du capteur de luminosité, les calculs ci-dessus sont effectués pour calculer le seuil théorique de radiation solaire. Si la valeur de radiation solaire mesurée est supérieur ou égale à 75% de la radiation solaire théorique alors on peut en conclure que le temps est ensoleillé.
A noter que ce calcul d'ensoleillement ne s'applique uniquement que lorsque l'inclinaison du soleil est supérieure à 3°. En effet, à l'approche du levé/couché du soleil, on atteind les limites de précisions de ces calculs.
Fichier excel:
Voici un extrait du fichier excel qui calcul pour chaque minute d'un jour donné les valeurs décrites ci-dessus.
Exemple:
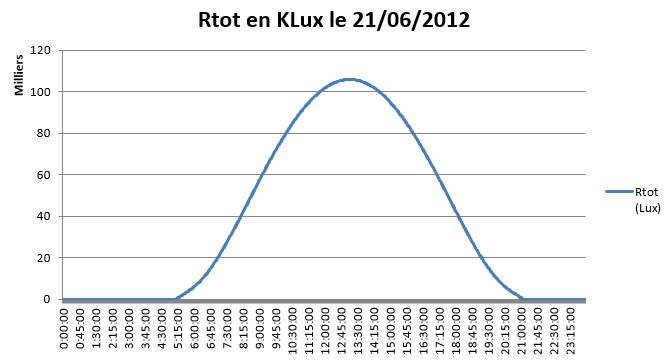
Code source
Voici un extrait du code source "SunCalculation.c" implémenté dans la plateforme linux embarqué que j'utilise.
Et le fichier include "SunCalculation.h" qui va avec :
Dernière mise à jour: 17/01/21